Etikett: Växtodling

Då man sitter och deklarerar så hittar man på allt möjligt för att för en stund slippa kvittona. Eftersom jag är gammal matematiker (låter litet som “astmatiker”) och jag länge retat mej på struntpratet om “optimal” gödsling så började jag göra en enkel matematisk analys av “optimal gödsling”.

Först gör man en massa antaganden som troligen inte stämmer men man måste få frågeställningen i matematisk form för att alls kunna gör en analys. Verkligheten är alldeles för invecklad. Så jag antog att lönsamhetskurvan är en upp-och-nedvänd parabol (x i kvadrat). På x-axeln (dn vågräta) finns den mängd pengar man sätter på gödsling och på y-axeln (den lodräta) de pengar man får in från skörden. Vi kan låtsas att 5 betyder 500 euro eller nånting – det exakta värdet har ingen betydelse för principen. Då får man inget alls in om man inte sätter ut nånting på gödsel. Här påpekar Mats direkt att det inte alls stämmer – vilket han har rätt i – men i en matematisk analys bryr man sej inte om småsaker :-). Det kallas att “abstrahera”.

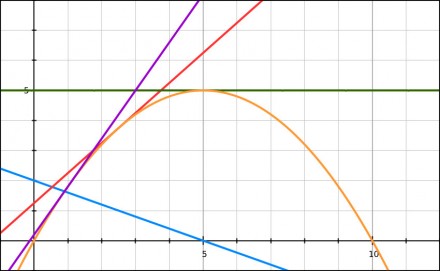
Parabolen är den gula kurvan. Det intressanta är emellertid hur mycket jag får in för varje euro jag lägger ut. Den största bruttoinkomsten får jag vid x=5 dvs. om jag lägger ut 500 euro så får jag in 500 euro. Det är ungefär där den största hektarskörden ligger. Sätter jag mera gödsel så börjar kemikalierna förgifta marken (ni har väl sett hur de bränner där en hop spillts ut ?)  och inkomsterna blir lägre trots större utgifter.

Men lönar det sej att sikta på maximal hektarskörd ? Tja, för gödselfirman lönar det sej nog men knappast för en bonde (om man inte ser det viktigaste i att kunna skryta för grannarna om sina stora hektarskördar – det är ju mänskligt). Om vi gör en matematisk analys så vill vi veta hur mycket mera man får in för varje satsad euro och då måste vi hitta derivatan för kurvan dvs. tangenten i kurvans olika punkter. Nu är det en smal sak att hitta derivatan (ifall  funktionen för kurvan alls går att derivera) och för x² är den 2x.  Eftersom den gula kurvan är vänd upp och ned och flyttad så får den funktionen -0.2(x-5)² +5 och derivatan blir -0.4(x -5). Derivatan är den blå linjen.

Derivatan visar direkt hur mycket jag får in för varje euro jag ger ut och vi ser att ur lönsamhetssynpunkt är det helst förkastligt att försöka få maximal hektarskörd. I x=5 är derivatan noll och ger man ut en euro till så får man ingen ökning alls i inkomsten. Även om det kan vara optimalt för Yara så är det absolut inte optimalt för oss.

Om vi går bakåt i kurvan (x blir mindre) så börjar derivatan stiga och i punkten x=2.5 så är derivatan 1 vilket betyder att vi för varje euro vi lägger ut får en euro tillbaka. Det leder inte direkt till någon förlust men inte heller till vinst. Var och en måste fundera ut om man vill satsa upp till den punkten. Jag gör det inte utan håller mej ordentligt under den. Den violetta linjen visar att gödsling med x=1 ger litet under två euro tillbaka då man satsar en euro.

Nu är ju den gula kurvan helt felaktig eftersom den går genom noll (som Mats helt riktigt påpekade enligt min fantasi). Men tanken var bara att visa principen för hur man beräknar “optimalt”. Och det viktigaste är att först definiera optimalt – för vem ?

I verkligheten finns det alltid näring i jorden så kurvan går aldrig genom nollpunkten. Problemet med verkligheten är att det inte finns någon gul kurva som passar alla alltid. Tvärtom så varierar kurvan från plats till plats och dessutom från tid till tid. Egentligen borde man kunna se in i framtiden för att veta hur “optimal” gödsling ser ut. Om man vet hurudant sommarens väder blir så kan man litet gissa sej till hur man borde gödsla. Här kommer erfarenheten in. Tyvärr säjer min erfarenhet från 60 års jordbruk (och väder) att man aldrig vet hur det blir. Farsan tyckte att det är bäst att gödsla måttligt och lika mycket varje år för det värsta är om man kommer i otakt med vädret och gödslar mycket de år det blir regnigt. Så dra man ned gödslingen nästa sommar – och så blir det torrt …

Nåja, inte var det här till någon nytta men det var roligt att pyssla litet med matematik som omväxling i kvittoradandet.

 

Nä, det är ingen bra idé att köra över ackumulatorn med tallriksharven – enda ursäkten är att det var mörkt. Det var alltså fotsteget som lossnade på stora Zetorn och ackumulatorlådan är fäst vid det. Så allt hamnade under bakhjulet och sedan under tallriksharven. Därefter hade jag en före detta ackumulator och en bucklig plåtlåda. Men eftersom en diesel inte behöver ström – annat än att starta – så gick det bra att köra hem.

Fotsteget satt fast med fyra stabila bultar men hade inget stöd så det vickade till varje gång man steg på det och till sist tröttnade metallen och brast. Bultarna höll nog men ramen under hytten gick sönder. Det var ju en korkad konstruktion som helt enkelt måste gå sönder. Då jag får höstbearbetningen klar så skall det svetsas fast stöd så att fotsteget inte kan röra sej.

Då jag berättade om olyckan så frågade dottern (svagt försmädligt) om jag inte märkt att fotsteget vinglade ? Jovisst, men som vanligt så tänkte jag att jag fixar det senare …

Ny acku hade jag hemma så det gick att reparera. Att banka tillbaka plåtlådan för ackun i sin gamla form var emellertid omöjligt. En skrynklig plåt får man aldrig rak igen. Men jag lyckades slå ut den så mycket att ackun ryms i lådan.

Annars så har det gått bra att köra med tallriksharven efter frosten. Nu börjar det emellertid bli så varmt att leran blir kladdig igen. Men jämför man med andra höstar så hålls harven riktigt ren. Jag har inte behövt laga ren den en enda gång i år än. Vissa höstar så klibbar leran fast så att man måste hacka lera efter ett par varv. Och lera blandad med halm kan bli stenhård.

Det värsta jag varit med om med tallriksharven var i alla fall då jag körde ett torrt augusti. Jag kom inte ens ett varv innan halmen lindats runt axlarna så att de inte alls rörde sej. Då är våta höstar bättre och tydligen bäst med litet frost (men inte för mycket).

Jag tror inte riktigt på direktsådd efter höstens regn. Det finns stora spår i leran och då den torkar på våren så kan det vara svårt att så. Med tallriksharven så jämnar man ut spåren och myllar dessutom ned halmen så den börjar förmultna. Det är inte så roligt på våren med stora mängder torr halm. Den torra halmen börjar nämligen släpas med såbillarna.

Det har varit lätt att köra med tallriksharven i år – lustigt nog. Nu har jag nästan alla “leidärlaand” (leråkrar) körda och mulljordarna är lättare att bearbeta även om det fryser på litet. Men tiodygnsprognosen lovar ganska varmt väder. Även om dagarna är korta så hinner man bra köra 5-7 hektar per dag utan att ha bråttom. Det beror litet på åkerns form. Om man måste backa och vända ofta så blir det långsammare.

 

 

Jag fick nyss höra att elstolparna skall tas bort och att det i stället blir jordkabel utmed vägen. Det var minsann goda nyheter. I hundra år har stolparna stått i vägen. Det gick an så länge vi bara körde med häst men då traktorerna kom så blev det problem. Speciellt skördetröskans tömningsrör och sprutans bom har fått sina törnar och är ganska krokiga.

Visst borde man vara försiktig och det går bra för det mesta men ibland då man kör mitt i natten för att de lovar regn så kan det hända att man inte ser stolparna förrän det är för sent. Sprutan igen är besvärlig därför att man inte kan köra långsammare vid stolpen  utan man måste hålla jämn hastighet så att spridningen blir jämn. Då måste man försöka stanna så nära stolpen man kan utan att det tar emot och tillika stänga av sprutan. Nå, det går illa ibland. Jag har inte kört sönder nån bom men visst är den litet tilltygad.

Sedan är ju stolparna härdar för kvickrot som därifrån sprider sej över åkern. Det är ganska omöjligt att bekämpa kvickroten runt stolparna effektivt.  Och fåglarna som sitter på trådarna sprider flyghavre på åkrarna. Så inte är man speciellt förtjust i eländet.

Och nu är det slut ! Ännu i höst skall stolparna bort.

Adjöss och kom aldrig tillbaka !